Md Ishat-E-Rabban

Md Ishat-E-Rabban

SDE at Intel | M.Sc. in CS from UMD College Park | Expert in Robotic Planning, Deep Learning, and Geometric Computing | Highly Proficient in C++ and Python

Heterogeneous Coordination using Particle Filters and Reinforcement Learning

Keywords: Reinforcement Learning, Proximal Policy Optimization, Particle Filters, Rapidly-Exploring Random Trees (RRTs), Receding Horizon Planning, Heterogenous (UGV-UAV) Coordination.

Source Code: Github

In this project, we investigate the performance of a heterogeneous multi-robot team consisting of one UAV (Unmanned Aerial Vehicle) and multiple UGVs (Unmanned Ground Vehicles) in the context of the Persistent Monitoring (PM) problem. More specifically, we are interested in determining how the knowledge of the position of other UGVs impacts the performance of the UGV team, and if the introduction of a UAV can reduce the positional uncertainty and thus improve task performance.

Persistent monitoring involves repeatedly visiting a given area, which has applications in patrolling, security surveillance, target searching, etc. In this work, we formulate a novel visibility-based PM problem where a team of UGVs equipped with cameras repeatedly patrols an obstructed 2D region. We call this the Visibility-based Persistent Monitoring (VPM) problem.

The design of an algorithm that plans the motion of the UGVs performing the VPM task depends on whether each UGV knows the position of all the other UGVs. In this work, we make the realistic assumption that the UGVs might not always maintain communication with one another, hence have incomplete information about the position of the other UGVs.

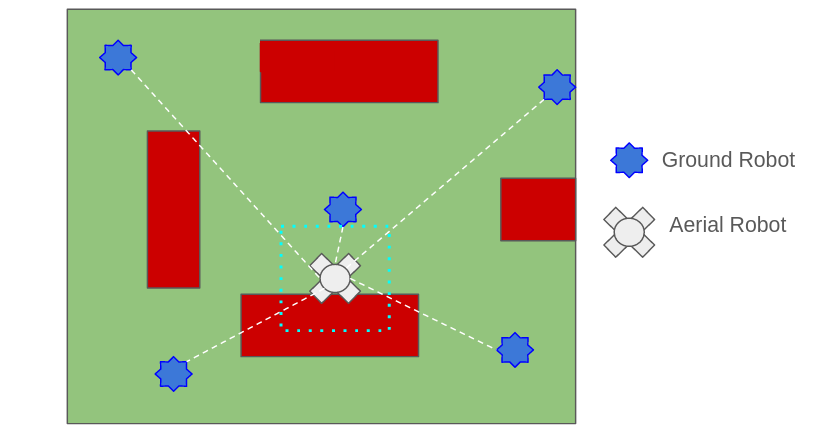
Another way of reducing the uncertainty in the position belief of the UGVs is to use a UAV as shown in the above figure. The UAV moves faster over the obstacles, locates UGVs within the environment, and communicates the acquired location information to all UGVs within its communication range. Thus each UGV has a better estimation of the positions of the other UGVs in comparison with the case where there is no UAV. Consequently, the UGVs can plan more knowledgeably while performing the VPM task.

UGV Planning

We model the uncertainty in position belief and latency belief as follows. Each UGV r maintains its individual local belief about the latency values of all the cells, which we call the Latency Belief of r. Also, r maintains it’s individual local belief about the positions of all UGVs, which we call the Position Belief of r. The latency belief is represented by a heat map over all the cells, and the position belief is represented as a set of particles as in the case of a Particle Filter. Note that, both the beliefs get updated when r comes within the communication range of some other robot and exchanges belief information. Maintaining a belief about the latency of the free grid cells and the position of the other UGVs helps each UGV to plan better while performing the VPM task. A visualization of the latency and position belief of a UGV is shown below.

To solve the UGV planning problem, we divide the time horizon into smaller planning rounds. At each planning round, we plan the path of each UGV in a distributed manner according to the latency and position belief of each UGV by employing Rapidly-exploring Random Trees (RRTs). This method of path planning is called Receding Horizon Planning.

We evaluate the performance of our UGV planning algorithm (VPM) against two algorithms. (1) The VPMT algorithm, in which each UGV knows the true location of all other UGVs. (2) The VPM-O algorithm, in which the UGVs neither know the position of the other UGVs, nor maintain a position belief. The experimental results are shown in the figure above.

UAV Planning

In our formulation of heterogeneous coordination, since a UGV does know the exact position of other UGVs, we use the UAV to sample and update the belief about all UGVs’ positions and use this shared information to assist the path planning of all UGVs. Thus UAV needs to plan a path that minimizes its uncertainty about UGVs’ positions and share this information with them.

The UAV planning problem is modeled using a Markov Decision Process (MDP), where the state is the heatmap generated by a particle filter-based algorithm, the set of actions is the four principal directions, the transition function is deterministic, and the reward function is given by the sum of latency values of all the cells.

We solve the above MDP using a Reinforcement Learning-based approach. We train an Actor-Critic version of Proximal Policy Optimization to investigate how the learning-based approach performs on the UAV path planning problem. The PPO takes as input the heatmap and outputs the action for the UAV. Our experimental findings suggest that the UAV effectively learns a policy over time as evidenced by the figure above.

Papers